射影平面についての導入的な話
この記事は 日曜数学会のadvent calender 21日目の記事です。
昨日はohtoyaさんの熱い記事でした。
自分の学生時代の数学の勉強を振り返って、何が難しかったかなあ、と考えると、まず「多様体難しかったな」と思うのです。何が難しかったかといえば、「何故このような概念を考えるのか」というところが分からず、そこで行われる議論を実感を持って理解できなかった、という点が大きいのではないかと思います。
今でも幾何には若干の苦手意識があり、あんまりしっかり理解できていない気持ちがあるのですが、それでも色々な勉強を経て、多様体が重要であるという気持ちは強く持っています。
そこで、今回は多様体に関連する話題として「当時こういうことをもっと考えておけば良かった」と思うことについて書きます。多様体の中で特に基本的な対象である射影平面のざっくりとした導入的な話です。
なお、今回の話では位相とか、微分構造とかについては深く考えないことにします。そういうことをあまり考えなくても今回扱う話題はわかると思うからです。ちゃんと考えたい方は『多様体の基礎(松本幸夫)』などの教科書をご覧ください。
1.射影平面とは?
まず、射影平面の定義をします。$R^3$の原点以外の$2$点$(x,y,z)$と$(x',y',z')$に対して、ある$\lambda \neq 0$が存在して$(x,y,z) = \lambda (x',y',z')$となるときに、この$2$点は同値であるとして同値関係を定めます。そして、この同値関係で$R^3$から原点を除いた集合を割った商集合を射影平面とします。$R^3$の原点を通る直線を一点だと思った集合だといっても良いです。
…と言ってもこれでは射影平面がどういうものか、イメージが湧きにくいのではないかと思います。そこでもう少しだけ実感が持てそうな捉え方を述べます。
まず、原点を通る直線は半径$1$の球面と必ず原点対称な$2$点で交わります。そこで、さらにこの$2$点を同一視してできるものが射影平面である、と見るわけです(下図で点Aと点Bを貼り付けることを、球面上の原点対称な$2$点全てで行う)。これは先ほどの「原点を通る直線を一点と思う」よりいくらか想像しやすいと思います。

2.射影平面は球面のように思い浮かべられない
ただ、そうは言ってもまだ射影平面は頭の中で思い浮かべにくいのではないかと思います。正直に言って、この見方で分かるのは「射影平面は球面の半分みたいなもの」という感覚くらいな気がします。実際、球面を上下に分けて原点対称な点を同一視していくと、球面の上半分だけ考えればよいことになり、さらにその境界である円周の原点対称な点を同一視することになりますが、そこで多くの人が「あれこの後どうなるの…?」となると思います。
実は射影平面を$R^3$の中で思い描くことは、球面のように単純にはできません。なんとか$R^3$内で描こうと思うと、自分自身と交わったりしてしまうので、うまく思い浮かべられなくなるのはある意味自然なのです。
例えば、射影平面をなんとか$R^3$の中に書く方法にboy's surfaceと呼ばれる曲面があります。参考までにboy's surfaceを作っている動画をあげますが、この後の話を理解する上では、こういった「なんとか$R^3$の中に描いた」イメージはむしろ理解の妨げになるように思いますので気にしないで大丈夫です(動画はすごく綺麗なのでオススメです)。
なお、射影平面は$R^4$には自分自身と交わらずに埋め込めることが知られています(whitney embedding theorem)ので、$4$次元まで行くと$R^3$の中の球面と同じように射影平面が存在していることが感じられるのかもしれません。でも、$4$次元は普通「見えない」ですよね(見える人がいたらどうやったら見えるようになるか伝授して欲しいです)。また、$4$次元でなら自分自身と交わらずに描ける、という事実もこの後の話を理解するためには必要がありません。
射影平面はこのように日常感覚からすると実在感が持ちにくい数学的対象で、そういうものを考えることに心理的な抵抗を持ちやすいと思います。しかし、こういうものの数学的な存在を認めることで物事が単純になることがあるため、ここでは「射影平面はあるんだ」と思うことにしましょう。
なお、射影平面は他にも一見異なるように見える作り方があります。こちらの佐野さんのブログには、様々な曲面の例と並んで射影平面が紹介されていて、こういうのを見ているとだんだん受け入れる気持ちが出てくるように思います(今回の記事の内容と重なる部分も多い面白い記事ですのでぜひお読みください)。
3.射影平面には平面が「すっぽり入る」
ここでは、この"変な"空間「射影平面$P^2(R)$」には、平面が「すっぽり入る」ことについて述べます。まず、射影平面では原点を通る直線を「一点」だと思っています。そこでこの直線から原点以外の一点$(x, y, z)$をとり、その直線を$[x: y: z]$で表すことにします。すると、射影平面は
$$ P^2(R)=\{[x: y: z]|(x, y, z) \neq (0,0,0) \} $$
と書くことができます。ここで射影平面のことを$P^2(R)$と書いています。$P$はprojectiveのPです。Pの右肩に載っている$2$は射影平面が$2$次元的な幾何学的対象であることから来ています。
さて、平面が射影平面$P^2(R)$に「すっぽり入る」というのは何を言いたいかというと、例えば平面を$R^3$内の平面$z=1$とした時、この平面から射影平面$P^2(R)$への
$$ (x,y,1) \in R^3 \mapsto [x:y:1] \in P^2(R) $$
という写像が単射である、ということです。単射、というのは$(x,y,1)$と$(x',y',1)$が異なるなら、写像の行き先も異なる、ということです。これは$(x,y,1)$と$(x',y',1)$が異なれば、原点とこれらの点を結ぶ直線も異なることから分かります。
さて、射影平面は全貌が頭の中で想像しがたい"変な"空間ですが、色々と興味深い性質を持っています。というか、興味深い性質を持っているので、多様体の授業でも基本的な例として取り上げられるのでしょう。その一つが「方程式を考えることができて、嬉しいことが起こる」というものです。
4.射影平面の中の方程式で定まる図形
このことを見るために、まず平面$z=1$と$xy$平面を同一視して、そこでの単位円について考えましょう。この式は$x^2 + y^2 =1$ですね(ただし$z=1$)。これはこんな図になります。
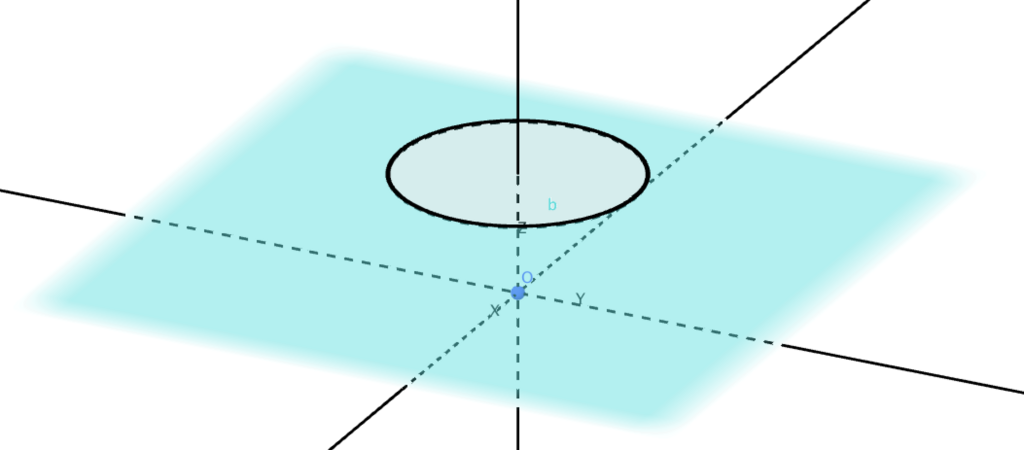
さて、この単位円の各点と原点を結ぶ直線を描くとどうなるでしょうか?答えはこんな感じになります。

そうです。円錐です。式で書けば$x^2 + y^2 = z^2$ となります。
さて、なぜ原点を結ぶ直線を考えたのか?というと、射影平面は原点を通る直線を一点だと思ったものと思えるのでした。したがって、この円錐の式$x^2 + y^2 = z^2$ は射影平面$P^2(R)$の中で意味を持つ式になっていて、この方程式の解集合は、(想像しがたい)射影平面$P^2(R)$の部分集合として一つの形を定めているのです!
つまり、
$$ \{[x:y:z] \in P^2(R) | x^2 + y^2 = z^2 \} \subset P^2(R) $$
です。
そして、その形は、私たちの思い浮かべることができる平面$z=1$の中の図形として見ると単位円になっている、ということになります。
さて、ここからこの射影平面の中で$x^2 + y^2 = z^2$という方程式が定める図形について考えて行きましょう。面白いのはここからです。ここまでは$z=1$という平面を考えていました。次に$y=1$という平面を考えてみます。これもやはり$P^2(R)$の中に「すっぽり入って」います。
つまりこの平面から射影平面$p^2(R)$への
$$ (x,1,z) \in R^3 \mapsto [x:1:z] \in P^2(R) $$
さて、では先ほど考えた射影平面の$x^2 +y^2 = z^2$という式が表す図形は、この対応を通して平面$y=1$の中の図形としてみるとどう見えるでしょうか?それは次のようになります。

式で書くと$x^2 + 1 = z^2$(ただし$y=1$)、つまり双曲線の式が現れます。さらに同じことを平面$z=x+1$で行うと次のように放物線が現れます。

さて、ここまでですでに気づいた方もいると思いますが、これは円錐を平面で切ると楕円、双曲線、放物線が現れる、という有名な事実の言い換えになっています!
つまり、「円錐を平面で切る」という行為が、「射影平面の$x^2 + y^2 = z^2$という方程式から定まる一つの図形を、射影平面の一部を切り取って(想像しやすい$R^3$内の)平面でみる」という行為にかわり、その切り取り方によって円が現れたり双曲線が現れたり、放物線が現れる、という風に言い換えられたわけです。
さて、このことから「射影平面という"変な"空間の存在を認めると、平面内の(非特異)二次曲線は射影平面の中での一つの図形、というか円を、切り取り方を変えて見ているだけ」という統一的な見方が示唆されます。そして、こう言った統一的な見方が得られることが射影平面の重要性の一つだと思います。
この見方から得られる面白い応用については今後改めて書いていくことにして、今日はこの辺で終わりにしたいと思います。お読みいただきありがとうございます。
明日はmattyuuさんが楕円曲線について何か書いてくれるそうです!お楽しみに!