「室外機問題」についての考察
こちらは12/6の日曜数学会のadvent calenderです。まず、投稿が遅れたことをtsujimotterさんにお詫びするとともに、このような機会を頂けたことを感謝します。また今回のテーマである「室外機問題」の考案者であり、この問題についてadvent calenderに書くことを快く許可して頂いた鯵坂もっちょさんにも感謝いたします。
「室外機問題」とは
一ヶ月くらい前のphicafe数学デーに参加した時に、鯵坂もっちょさんから「室外機問題」という問題を教えてもらいました。その問題は身近な日常の問題を数学的に考えるもので、なんとなく興味を惹かれて最近チラチラと考えていたのですが、見通しよく解けることが分かったので、今回はそれについて書きます。

なお、「室外機問題」は私が考えるより前に数学デーで解かれている問題で、ここに書くことはもしかしたらその時に考えられていた皆さまの考察の範囲内なのかもしれませんが、以下に書く内容は自分で考えたものなので、お許しを。
さて、「室外機問題」とは次のような問題です:
「真夏の蒸し暑い夜、B氏はマンションの一室で寝ようとしている。B氏はエアコンが嫌いなため、窓を開けて寝ようとした。しかし、両隣の部屋の住人がエアコンをつけているようで、両隣の部屋のベランダに置かれた2つの室外機がブォンブォンと音を出し、B氏の睡眠を妨げている。
2つの室外機をとしよう。室外機
は5分音を出したのち5分静かになり、を10分の周期で繰り返し、室外機
は7分音を出したのち7分静かになり、を14分の周期で繰り返しているとする。この時、室外機の音が無い(B氏が静かな時間を過ごせる)時間の割合はどれだけあるか?ただし、簡単のため、2つの室外機が動き始めたタイミングは揃っているとする。」
(元々の問題の細部は忘れてしまったので、数学的内容が変わらない範囲で創作しています)

「室外機問題」の解法
以下ではこの問題とその一般化の解法を書きます。この問題を考えていて個人的にグッときたポイントを先に書いておくと、この問題は初等整数論や、代数学の初歩的な知識を用いることにより、スッキリ捉えることができます。
室外機の出す音の周期的な挙動を、
を使って表しましょう。室外機
が最初の5分は音が出て、後半の5分は音が無い、という状況を、音が出ない時間に注目して
で表すことにします。同様に、室外機
の状況を、音が出ない時間に注目して
で表します。
室外機は周期
を持つ(「分」は省略しました)ので、この二つを合わせると周期70(=10と14の最小公倍数)で音の有る無しの挙動が繰り返されます。このうちの音が無い時間がどれだけあるかを求めたいわけです。そこで、周期70で音が無い時間全体を
と置きます。この時、室外機の音が無い時間の割合は
なので、
が求まればこの問題は解けたことになります。
さて、周期70のうちのあるタイミングで音が無かった(つまり
)としましょう。この条件は、
をmod 10で見直すと
であり、かつ、mod 14で見直すと
になる、という条件と同値です。
この状況を一般化した上で、写像の言葉を使って書き直します:
室外機の周期を
、室外機
の周期を
とし、
を
の部分集合とする。 また、
の最小公倍数を
とする。
写像を、
\begin{align}
\phi(x)=(x \hspace{2mm} \text{mod }N_1,x \hspace{2mm} \text{mod }N_2)
\end{align}
と定めると、これはアーベル群の準同型写像であり、
\begin{align}
x \in S \Leftrightarrow \phi(x) \in S_1 \times S_2
\end{align}
となる。
次にこの条件を、問題が解きやすくなるように書き換えていきます:
まず、
\begin{align}
\phi(x) \in S_1 \times S_2 \Leftrightarrow x \in \phi^{-1}(S_1 \times S_2)
\end{align}
なので、
\begin{align}
S=\phi^{-1}(S_1 \times S_2)
\end{align}
です。
今必要なのはなので、
が分かれば良いのですが、ここで
は単射であることがすぐに分かる(
が10でも14でも割り切れるなら、70でも割り切れる)ので、
\begin{align}
|\phi^{-1}(S_1 \times S_2)|&=|\phi(\phi^{-1}(S_1 \times S_2))|\\
&=|\text{Im}\phi \cap S_1 \times S_2 |
\end{align}
となります。
従って、色々と書いてきましたが、この問題を解くには、(は最初に与えられているデータなので)結局
が何なのかがわかれば良いことになります。
そして、これについて、とても都合の良い初等整数論の次の命題が成り立ちます:
命題1. を
の最大公約数とし、写像
を
\begin{align}
\psi(x_1,x_2)=x_1 \hspace{2mm}\text{mod }D - x_2\hspace{2mm}\text{mod }D
\end{align}
と定める。この時、以下は完全:
\begin{align}
0{ \longrightarrow } \mathbb{Z}/L\mathbb{Z} \stackrel { \phi } { \longrightarrow } \mathbb{Z}/N_1\mathbb{Z} \times \mathbb{Z}/N_2\mathbb{Z} \stackrel { \psi } { \longrightarrow } \mathbb{Z}/D\mathbb{Z} \rightarrow 0.
\end{align}
(証明の概略)が単射であることは上で触れたのと同様に分かる。
が全射であること、
は明らか。また、
より
となり、両者は一致する。(証明の概略終了)
Remark. 証明中に(2つの正の整数の積はその最小公倍数と最大公約数の積に等しい)というよく知られた事実を用いましたが、この命題はこの事実のアーベル群バージョンと見ることができると思います。また、
が互いに素なら中国剰余定理の特別な場合になっていて、中国剰余定理の仲間に位置付けられる命題でもあります。
さて、この命題を用いて「室外機問題」を解きます。命題1より、求めたかったは
に等しく、
の定義よりそれは
\begin{align}
x_1 \equiv x_2 \hspace{2mm}\text{mod }D
\end{align}
を満たす 全体となります。つまり、
\begin{align}
|S|=|\{(x_1,x_2 ) \in S_1 \times S_2 \hspace{1mm}|\hspace{1mm} x_1 \equiv x_2 \hspace{2mm}\text{mod }D \}|
\end{align}
によりが求められます。
これを最初の問題設定で具体的に求めてみると、より
であり、
の元のうち、各成分の偶奇が一致しているもの、つまり
\begin{align}
\{6,8\} \times \{8,10,12\} \cup \{5,7,9\} \times \{7,9,11,13\}
\end{align}
の元の個数が求めるとなります。よって、
です。以上より室外機の音が無い時間の割合は18/70≒25.7%となり、問題はめでたく解決されました。
…と、ここまでたどり着いた瞬間はとても嬉しかったのですが、今この記事を書いていて、なんだかすごく当たり前のことをしただけのように思えてきました。自分の考えたことなんて何も無かったのではないか、、というような。数学を勉強していると良くあることです。
しかし、勢いに任せて当初書こうと思っていたことを一通り書こうと思います。
「室外機問題」の一般化およびその解法
問題をさらに次のように一般化します。室外機が台あり、その周期や音がでるタイミングもバラバラだとしましょう。この時に全ての室外機が音を出していない静かな時間
はどのように求められるでしょうか?

台の室外機のそれぞれの周期を
(ただし、
たちは全て正の整数)とし、それぞれの室外機についての音の無い時間が
で指定されているとします。また、
台の室外機全体の周期
の中で、音が無い時間全体を
と置きます。上記と同様に、写像
を、
\begin{align}
\phi(x)=(x \hspace{2mm} \text{mod }N_1,\cdots,x \hspace{2mm} \text{mod }N_k)
\end{align}
とすると、は
に一致します。また、
は単射もすぐに分かるので、
\begin{align}
|\phi^{-1}(S_1 \times S_2 \times \cdots S_k)|&=|\phi(\phi^{-1}(S_1 \times S_2 \times \cdots S_k))|\\
&=|\text{Im}\phi \cap S_1 \times S_2 \times \cdots S_k |
\end{align}
となります。 従ってこの場合にもが分かれば良いことになります。さらに、これについても、上記の命題1を一般化した次の命題が成り立ちます:
命題2. を
と
の最大公約数とし、写像
を
\begin{align}
\psi(x_1,\cdots,x_k)=(\cdots,x_i \hspace{2mm}\text{mod }D_{ij} - x_j\hspace{2mm}\text{mod }D_{ij},\cdots)
\end{align}
と定める。この時、以下は完全:
\begin{align}
0{ \longrightarrow } \mathbb{Z}/L\mathbb{Z} \stackrel { \phi } { \longrightarrow } \mathbb{Z}/N_1\mathbb{Z} \times \cdots \times \mathbb{Z}/N_k\mathbb{Z} \stackrel { \psi } { \longrightarrow } \prod_{i , j} \mathbb{Z}/D_{ij} \mathbb{Z} .
\end{align}
(証明は省略。気になる方は高木貞治, 初等整数論講義 第2版, 共立出版, 第1章§6. [問題 2] などを参照されると良いと思います。)
この命題より、「一般化された室外機問題」も解決されました。つまり、与えられたの元
のうち、全てのi,jで
\begin{align}
x_i \equiv x_j \hspace{2mm}\text{mod }D_{ij}
\end{align}
を満たすものの個数が求めるの値となります:
\begin{align}
|S|=|\{(x_1,\cdots,x_k ) \in S_1 \times \cdots\times S_k \hspace{1mm}|\hspace{1mm} x_i \equiv x_j \hspace{2mm}\text{mod }D_{i,j} \hspace{2mm}(i,j=1,\cdots,k) \}|.
\end{align}
kが増えれば手順は室外機が2個の時よりも複雑にはなりますが、この方法で求めることができます。
最後に
これでこの一般化に対する「室外機問題」はできたと思うのですが、「室外機問題」自体はまだまだ考える余地がある面白い問題だと思います。
例えば、今回は周期が正の整数で、室外機が動き出すタイミングも揃っている前提で考えましたが、そうではなく、周期が無理数のものが混じっていたり、動き出すタイミングが揃っていない場合に、音の出ない時間の割合や集合がどのようなものになるか、という問題は興味深いと思います。
また、これはもはや「室外機問題」と関係ないかもしれないのですが、個人的に一番気になっているのは、命題1や命題2で出てきた完全系列は、層( 層 (数学) - Wikipedia )の定義を完全系列を用いて書いたものによく似ているということです。
これらの命題は本質的には高木貞治, 初等整数論講義の第1章§6. [問題 1][問題 2]の内容なのですが、今回問題を考えている際にそれを上記のような完全系列に書いてみたところ、層の定義ととても似ていることに気づきました。
実際、命題1の完全系列の場合は3点集合に適当な位相を入れた時の層の条件とみなすことができるのですが、これは一般的に言えることなのでしょうか?
本当はこれについて理解して書くことも記事のモチベーションだったのですが、一般の場合はすぐには分からなかったので一旦記事をアップします。もしご存知の方がいましたら教えていただけると幸いです。
それではお読みいただきありがとうございます。
Nekrasov-Okounkov多項式
Nekrasov-Okounkov formulaの$x^n(n \geq 1)$の係数として現れる$z$の多項式を$n$次のNekrasov-Okunkov多項式と呼ぶことにする。
私にとってNekrasov-Okounkov formulaは衝撃的で、Nekrasov-Okounkov多項式もきっと奥深い性質を持っているに違いないと思っているので、この多項式についてとりあえず今分かることをメモする。
$n$次のNekrasov-Okounkov多項式について比較的すぐに分かること:
・最高次の項は$(-z)^n/n!$
−なお、これとNekrasov-Okounkov formulaと併せると、$$ \sum_{\lambda \in \mathcal{P}(n)} \left( \frac{n!}{\prod_{h \in \mathcal{H}(\lambda)} h} \right)^2 =n!$$
が分かる。これは$S_n$の既約表現についてのhook length formulaから出る等式と見ることもできる。
・定数項は$P(n)$(分割数)
・$n$次のNekrasov-Okounkov多項式が$1$以上の整数解$k$を持つことと、無限積$$ \prod_{l=1}^{\infty} (1-x^l)^{k - 1} $$
を展開した時の$x^{n}$の項は消えることは同値。
− したがって、Nekrasov-Okounkov多項式は常に$z=1$を解に持つ
− 同様に、Eulerの五角数定理より$n$が五角数でない限り、$n$次のNekrasov-Okounkov多項式は$z=2$を解に持つ
− 同様に、Jacobiによる三角数定理(この呼び名が通称として相応しいのかは不明)より、$n$が三角数でない限り、$n$次のNekrasov-Okounkov多項式は$z=4$を解に持つ
とりあえず今分かることはこれくらい。
また、$n=25$までのNekrasov-Okounkov多項式は以下の通り:
n=1:$$-z+1$$
n=2:$$\frac{1}{2!} \left(z - 4\right) \left(z - 1\right) $$
n=3:$$- \frac{1}{3!} \left(z - 9\right) \left(z - 2\right) \left(z - 1\right)$$
n=4:$$\frac{1}{4!} \left(z - 15\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right)$$
n=5:$$- \frac{1}{5!} \left(z - 7\right) \left(z - 4\right) \left(z - 1\right) \left(z^{2} - 23 z + 30\right)$$
n=6:$$\frac{1}{6!} \left(z - 11\right) \left(z - 2\right) \left(z - 1\right) \left(z^{3} - 37 z^{2} + 252 z - 360\right)$$
n=7:$$-\frac{1}{7!} \left(z - 9\right) \left(z - 4\right) \left(z - 3\right) \left(z - 1\right) \left(z^{3} - 53 z^{2} + 632 z - 700\right)$$
n=8:$$\frac{1}{8!} \left(z - 7\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{4} - 78 z^{3} + 1799 z^{2} - 13362 z + 15840\right)$$
n=9:$$- \frac{1}{9!} \left(z - 27\right) \left(z - 15\right) \left(z - 5\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{3} - 63 z^{2} + 614 z - 672\right)$$
n=10:$$\frac{1}{10!} \left(z - 2\right) \left(z - 1\right) \left(z^{8} - 142 z^{7} + 7462 z^{6} - 189700 z^{5} + 2551129 z^{4} - 18486958 z^{3} + 69956928 z^{2} - 123511680 z + 76204800\right)$$
n=11:$$- \frac{1}{11!} \left(z - 9\right) \left(z - 4\right) \left(z - 3\right) \left(z - 2\right) \left(z - 1\right) \left(z^{6} - 157 z^{5} + 8827 z^{4} - 223807 z^{3} + 2603236 z^{2} - 11829700 z + 10348800\right)$$
n=12:$$\frac{1}{12!} \left(z - 4\right) \left(z - 3\right) \left(z - 1\right) \left(z^{9} - 202 z^{8} + 15734 z^{7} - 617728 z^{6} + 13385669 z^{5} - 163892398 z^{4} + 1108290916 z^{3} - 3830496072 z^{2} + 5760629280 z - 3073593600\right)$$
n=13:$$- \frac{1}{13!} \left(z - 11\right) \left(z - 9\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{8} - 220 z^{7} + 18286 z^{6} - 736780 z^{5} + 15287629 z^{4} - 158605480 z^{3} + 735371844 z^{2} - 1357495920 z + 794102400\right)$$
n=14:$$\frac{1}{14!} \left(z - 7\right) \left(z - 5\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{9} - 268 z^{8} + 28354 z^{7} - 1544872 z^{6} + 47316409 z^{5} - 829931452 z^{4} + 8055057156 z^{3} - 38844159408 z^{2} + 71529950880 z - 42032390400\right)$$
n=15:$$- \frac{1}{15!} \left(z - 15\right) \left(z - 9\right) \left(z - 1\right) \left(z^{12} - 305 z^{11} + 37226 z^{10} - 2381350 z^{9} + 87915033 z^{8} - 1946477505 z^{7} + 26139160508 z^{6} - 213047751640 z^{5} + 1052551647616 z^{4} - 3112765983440 z^{3} + 5308804041216 z^{2} - 4745959061760 z + 1704819916800\right)$$
n=16:$$\frac{1}{16!} \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{13} - 369 z^{12} + 56543 z^{11} - 4756065 z^{10} + 244577013 z^{9} - 8099449767 z^{8} + 177046581389 z^{7} - 2572836067755 z^{6} + 24670734911686 z^{5} - 152556756319164 z^{4} + 582735184849368 z^{3} - 1277681108424480 z^{2} + 1415868516921600 z - 604145558016000\right)$$
n=17:$$- \frac{1}{17!} \left(z - 11\right) \left(z - 7\right) \left(z - 4\right) \left(z - 3\right) \left(z - 2\right) \left(z - 1\right) \left(z^{11} - 397 z^{10} + 64956 z^{9} - 5756358 z^{8} + 305173737 z^{7} - 10071035433 z^{6} + 208090543154 z^{5} - 2629866062372 z^{4} + 19152433219752 z^{3} - 71477431676640 z^{2} + 110874456979200 z - 57164050944000\right)$$
n=18:$$\frac{1}{18!} \left(z - 9\right) \left(z - 4\right) \left(z - 3\right) \left(z - 2\right) \left(z - 1\right) \left(z^{13} - 458 z^{12} + 88277 z^{11} - 9457990 z^{10} + 626609703 z^{9} - 26999339214 z^{8} + 773862451151 z^{7} - 14813045077450 z^{6} + 187035483154996 z^{5} - 1510624401677528 z^{4} + 7380786567804672 z^{3} - 19832824586136960 z^{2} + 24912334784332800 z - 11411638318080000\right)$$
n=19:$$- \frac{1}{19!} \left(z - 15\right) \left(z - 9\right) \left(z - 7\right) \left(z - 5\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{12} - 489 z^{11} + 100058 z^{10} - 11269590 z^{9} + 772773513 z^{8} - 33648079257 z^{7} + 939541565804 z^{6} - 16552578568920 z^{5} + 175713524447536 z^{4} - 1028365456921104 z^{3} + 2871533166977088 z^{2} - 3564237339210240 z + 1576880931225600\right)$$
n=20:$$\frac{1}{20!} \left(z - 27\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{16} - 556 z^{15} + 131848 z^{14} - 17643604 z^{13} + 1486404394 z^{12} - 83318960668 z^{11} + 3203887810904 z^{10} - 85937102481692 z^{9} + 1619937615235709 z^{8} - 21459496970724296 z^{7} + 198286994819857448 z^{6} - 1257550544665186304 z^{5} + 5327095987955967696 z^{4} - 14440964737559690880 z^{3} + 23418660883299552000 z^{2} - 20222278886363904000 z + 7062173884846080000\right)$$
n=21:$$- \frac{1}{21!} \left(z - 3\right) \left(z - 2\right) \left(z - 1\right) \left(z^{18} - 645 z^{17} + 181164 z^{16} - 29411460 z^{15} + 3089705262 z^{14} - 222789954870 z^{13} + 11412738495268 z^{12} - 423984857498340 z^{11} + 11556588222302073 z^{10} - 232262704837309725 z^{9} + 3439428837461673672 z^{8} - 37294228226926193040 z^{7} + 292476205418706388864 z^{6} - 1626275436182757587760 z^{5} + 6220237978739694136896 z^{4} - 15631227078519704636160 z^{3} + 24015234457861808716800 z^{2} - 19941448143554638848000 z + 6744004366665646080000\right)$$
n=22:$$\frac{1}{22!} \left(z - 4\right) \left(z - 3\right) \left(z - 1\right) \left(z^{19} - 707 z^{18} + 218934 z^{17} - 39424308 z^{16} + 4622819982 z^{15} - 374541857634 z^{14} + 21709783422808 z^{13} - 919486583621396 z^{12} + 28807777191625113 z^{11} - 671551479927955011 z^{10} + 11653577399478528282 z^{9} - 149859859390837409184 z^{8} + 1414271918322614932624 z^{7} - 9642559353124617228848 z^{6} + 46417524835311084386976 z^{5} - 152732930419688742410112 z^{4} + 328362843132027552257280 z^{3} - 432364135808296502092800 z^{2} + 312231350735689448448000 z - 93854060769430241280000\right)$$
n=23:$$- \frac{1}{23!} \left(z - 9\right) \left(z - 7\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{18} - 759 z^{17} + 252558 z^{16} - 48873660 z^{15} + 6152394342 z^{14} - 533850545778 z^{13} + 33001140423136 z^{12} - 1480891076495820 z^{11} + 48685114324498113 z^{10} - 1174610230572239967 z^{9} + 20693922547850168154 z^{8} - 263095975592270942880 z^{7} + 2367665368264015376944 z^{6} - 14667220640957936756496 z^{5} + 60242233084184512189152 z^{4} - 156333564339685864496640 z^{3} + 240134231530973642457600 z^{2} - 195686055548754236928000 z + 64373573427183820800000\right)$$
n=24:$$\frac{1}{24!} \left(z - 15\right) \left(z - 5\right) \left(z - 4\right) \left(z - 2\right) \left(z - 1\right) \left(z^{19} - 825 z^{18} + 299910 z^{17} - 63750900 z^{16} + 8867572926 z^{15} - 855804488070 z^{14} + 59280627791320 z^{13} - 3006928989398700 z^{12} + 112924440704234841 z^{11} - 3153430914698846265 z^{10} + 65397488365073184330 z^{9} - 1000720519216019309400 z^{8} + 11165946141511470389536 z^{7} - 89231390122026577938960 z^{6} + 497883652140867053502240 z^{5} - 1872575280998611549056000 z^{4} + 4523913554083642562397696 z^{3} - 6563815484718982000250880 z^{2} + 5113041561388142523187200 z - 1628677054549753528320000\right)$$
n=25:$$- \frac{1}{25!} \left(z - 4\right) \left(z - 3\right) \left(z - 2\right) \left(z - 1\right) \left(z^{21} - 915 z^{20} + 372665 z^{19} - 89778825 z^{18} + 14340801396 z^{17} - 1613683271430 z^{16} + 132645337281730 z^{15} - 8150918464226850 z^{14} + 379971969347508281 z^{13} - 13557480534509026095 z^{12} + 371853588020715429045 z^{11} - 7843715715836597066325 z^{10} + 126826050927101544683746 z^{9} - 1560686931429962677584360 z^{8} + 14446840026729908781222560 z^{7} - 98871580481053579526898000 z^{6} + 488044196688548328227676576 z^{5} - 1677349781800446047971507200 z^{4} + 3815333842055999879911104000 z^{3} - 5328722678891290505003520000 z^{2} + 4050811077622468999741440000 z - 1265456219368419606528000000\right)$$
Nekrasov-Okounkovの公式
調べ物をしていてすごい等式を知ったのでメモ。
Nekrasov-Okounkovの公式
$z$を複素数とする。
$$ \prod_{k=1}^{\infty} (1-x^k)^{z-1} = \sum_{\lambda \in \mathcal{P}} \left( \prod_{h \in \mathcal{H}(\lambda)}(1-\frac{z}{h^2}) \right) x^{|\lambda|} $$
が成り立つ。ここで$\mathcal{P}$は分割の集合($0$以上の整数 $n$の分割の集合$\mathcal{P}(n)$の和集合)、$\mathcal{H}(\lambda)$は分割$\lambda$のhook長からなる多重集合。
$z$が複素数というのにびっくりした。
http://www.numdam.org/article/AIF_2010__60_1_1_0.pdf
にはこの公式を$A_{\it{l}}^{\alpha}$のMacdonald identitiesから導く証明が載っている。
そもそも、Macdonald identities自体がすごい等式なのでここに書いておく($A_{\it{l}}^{\alpha}$のケースのみ)。
Macdonald identities
$t=2t'+1$を正の奇数とする。
$$ η (x)^{t^2-1} = \frac{(-1)^{t'}}{1!2! \cdots (t-1)!} \sum_{(v_0,v_1,\cdots,v_{t-1}) \in V_t} \left( \prod_{ i < j } (v_i - v_j) \right) x^{(v_0^2 + v_1^2 + \cdots + v_{t-1}^2)/(2t)} $$
が成り立つ。 ここで$ η (x)$はデデキントのエータ関数。また、$V_t$は次の二つの条件を満たす整数の組$(v_0,v_1,\cdots,v_{t-1})$の集合:
1. $v_i \equiv i \hspace{2mm} (\text{mod } t)$
2. $v_0 + v_1 + \cdots + v_{t-1} = 0$
証明など詳細が気になる人は上記の論文を見てください。
射影平面についての導入的な話
この記事は 日曜数学会のadvent calender 21日目の記事です。
昨日はohtoyaさんの熱い記事でした。
自分の学生時代の数学の勉強を振り返って、何が難しかったかなあ、と考えると、まず「多様体難しかったな」と思うのです。何が難しかったかといえば、「何故このような概念を考えるのか」というところが分からず、そこで行われる議論を実感を持って理解できなかった、という点が大きいのではないかと思います。
今でも幾何には若干の苦手意識があり、あんまりしっかり理解できていない気持ちがあるのですが、それでも色々な勉強を経て、多様体が重要であるという気持ちは強く持っています。
そこで、今回は多様体に関連する話題として「当時こういうことをもっと考えておけば良かった」と思うことについて書きます。多様体の中で特に基本的な対象である射影平面のざっくりとした導入的な話です。
なお、今回の話では位相とか、微分構造とかについては深く考えないことにします。そういうことをあまり考えなくても今回扱う話題はわかると思うからです。ちゃんと考えたい方は『多様体の基礎(松本幸夫)』などの教科書をご覧ください。
1.射影平面とは?
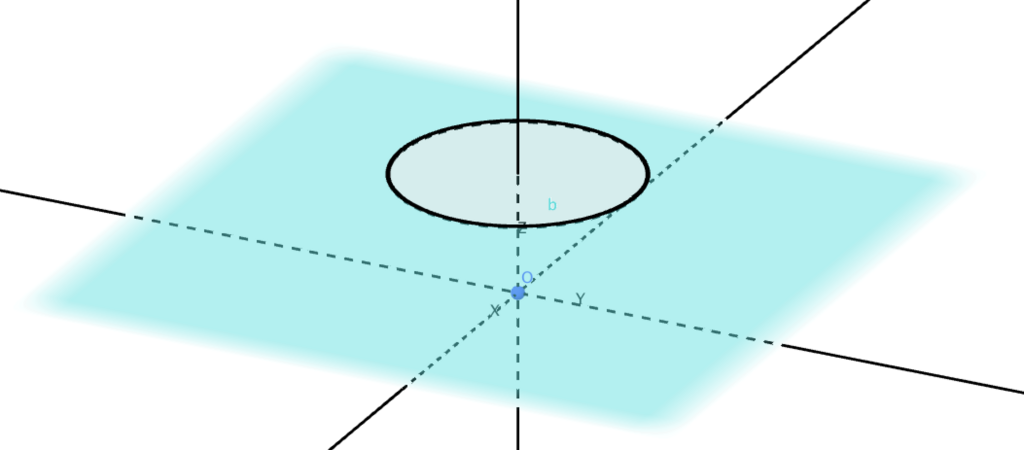
まず、射影平面の定義をします。$R^3$の原点以外の$2$点$(x,y,z)$と$(x',y',z')$に対して、ある$\lambda \neq 0$が存在して$(x,y,z) = \lambda (x',y',z')$となるときに、この$2$点は同値であるとして同値関係を定めます。そして、この同値関係で$R^3$から原点を除いた集合を割った商集合を射影平面とします。$R^3$の原点を通る直線を一点だと思った集合だといっても良いです。
…と言ってもこれでは射影平面がどういうものか、イメージが湧きにくいのではないかと思います。そこでもう少しだけ実感が持てそうな捉え方を述べます。
まず、原点を通る直線は半径$1$の球面と必ず原点対称な$2$点で交わります。そこで、さらにこの$2$点を同一視してできるものが射影平面である、と見るわけです(下図で点Aと点Bを貼り付けることを、球面上の原点対称な$2$点全てで行う)。これは先ほどの「原点を通る直線を一点と思う」よりいくらか想像しやすいと思います。

2.射影平面は球面のように思い浮かべられない
ただ、そうは言ってもまだ射影平面は頭の中で思い浮かべにくいのではないかと思います。正直に言って、この見方で分かるのは「射影平面は球面の半分みたいなもの」という感覚くらいな気がします。実際、球面を上下に分けて原点対称な点を同一視していくと、球面の上半分だけ考えればよいことになり、さらにその境界である円周の原点対称な点を同一視することになりますが、そこで多くの人が「あれこの後どうなるの…?」となると思います。
実は射影平面を$R^3$の中で思い描くことは、球面のように単純にはできません。なんとか$R^3$内で描こうと思うと、自分自身と交わったりしてしまうので、うまく思い浮かべられなくなるのはある意味自然なのです。
例えば、射影平面をなんとか$R^3$の中に書く方法にboy's surfaceと呼ばれる曲面があります。参考までにboy's surfaceを作っている動画をあげますが、この後の話を理解する上では、こういった「なんとか$R^3$の中に描いた」イメージはむしろ理解の妨げになるように思いますので気にしないで大丈夫です(動画はすごく綺麗なのでオススメです)。
なお、射影平面は$R^4$には自分自身と交わらずに埋め込めることが知られています(whitney embedding theorem)ので、$4$次元まで行くと$R^3$の中の球面と同じように射影平面が存在していることが感じられるのかもしれません。でも、$4$次元は普通「見えない」ですよね(見える人がいたらどうやったら見えるようになるか伝授して欲しいです)。また、$4$次元でなら自分自身と交わらずに描ける、という事実もこの後の話を理解するためには必要がありません。
射影平面はこのように日常感覚からすると実在感が持ちにくい数学的対象で、そういうものを考えることに心理的な抵抗を持ちやすいと思います。しかし、こういうものの数学的な存在を認めることで物事が単純になることがあるため、ここでは「射影平面はあるんだ」と思うことにしましょう。
なお、射影平面は他にも一見異なるように見える作り方があります。こちらの佐野さんのブログには、様々な曲面の例と並んで射影平面が紹介されていて、こういうのを見ているとだんだん受け入れる気持ちが出てくるように思います(今回の記事の内容と重なる部分も多い面白い記事ですのでぜひお読みください)。
3.射影平面には平面が「すっぽり入る」
ここでは、この"変な"空間「射影平面$P^2(R)$」には、平面が「すっぽり入る」ことについて述べます。まず、射影平面では原点を通る直線を「一点」だと思っています。そこでこの直線から原点以外の一点$(x, y, z)$をとり、その直線を$[x: y: z]$で表すことにします。すると、射影平面は
$$ P^2(R)=\{[x: y: z]|(x, y, z) \neq (0,0,0) \} $$
と書くことができます。ここで射影平面のことを$P^2(R)$と書いています。$P$はprojectiveのPです。Pの右肩に載っている$2$は射影平面が$2$次元的な幾何学的対象であることから来ています。
さて、平面が射影平面$P^2(R)$に「すっぽり入る」というのは何を言いたいかというと、例えば平面を$R^3$内の平面$z=1$とした時、この平面から射影平面$P^2(R)$への
$$ (x,y,1) \in R^3 \mapsto [x:y:1] \in P^2(R) $$
という写像が単射である、ということです。単射、というのは$(x,y,1)$と$(x',y',1)$が異なるなら、写像の行き先も異なる、ということです。これは$(x,y,1)$と$(x',y',1)$が異なれば、原点とこれらの点を結ぶ直線も異なることから分かります。
さて、射影平面は全貌が頭の中で想像しがたい"変な"空間ですが、色々と興味深い性質を持っています。というか、興味深い性質を持っているので、多様体の授業でも基本的な例として取り上げられるのでしょう。その一つが「方程式を考えることができて、嬉しいことが起こる」というものです。
4.射影平面の中の方程式で定まる図形
このことを見るために、まず平面$z=1$と$xy$平面を同一視して、そこでの単位円について考えましょう。この式は$x^2 + y^2 =1$ですね(ただし$z=1$)。これはこんな図になります。
さて、この単位円の各点と原点を結ぶ直線を描くとどうなるでしょうか?答えはこんな感じになります。

そうです。円錐です。式で書けば$x^2 + y^2 = z^2$ となります。
さて、なぜ原点を結ぶ直線を考えたのか?というと、射影平面は原点を通る直線を一点だと思ったものと思えるのでした。したがって、この円錐の式$x^2 + y^2 = z^2$ は射影平面$P^2(R)$の中で意味を持つ式になっていて、この方程式の解集合は、(想像しがたい)射影平面$P^2(R)$の部分集合として一つの形を定めているのです!
つまり、
$$ \{[x:y:z] \in P^2(R) | x^2 + y^2 = z^2 \} \subset P^2(R) $$
です。
そして、その形は、私たちの思い浮かべることができる平面$z=1$の中の図形として見ると単位円になっている、ということになります。
さて、ここからこの射影平面の中で$x^2 + y^2 = z^2$という方程式が定める図形について考えて行きましょう。面白いのはここからです。ここまでは$z=1$という平面を考えていました。次に$y=1$という平面を考えてみます。これもやはり$P^2(R)$の中に「すっぽり入って」います。
つまりこの平面から射影平面$p^2(R)$への
$$ (x,1,z) \in R^3 \mapsto [x:1:z] \in P^2(R) $$
さて、では先ほど考えた射影平面の$x^2 +y^2 = z^2$という式が表す図形は、この対応を通して平面$y=1$の中の図形としてみるとどう見えるでしょうか?それは次のようになります。

式で書くと$x^2 + 1 = z^2$(ただし$y=1$)、つまり双曲線の式が現れます。さらに同じことを平面$z=x+1$で行うと次のように放物線が現れます。

さて、ここまでですでに気づいた方もいると思いますが、これは円錐を平面で切ると楕円、双曲線、放物線が現れる、という有名な事実の言い換えになっています!
つまり、「円錐を平面で切る」という行為が、「射影平面の$x^2 + y^2 = z^2$という方程式から定まる一つの図形を、射影平面の一部を切り取って(想像しやすい$R^3$内の)平面でみる」という行為にかわり、その切り取り方によって円が現れたり双曲線が現れたり、放物線が現れる、という風に言い換えられたわけです。
さて、このことから「射影平面という"変な"空間の存在を認めると、平面内の(非特異)二次曲線は射影平面の中での一つの図形、というか円を、切り取り方を変えて見ているだけ」という統一的な見方が示唆されます。そして、こう言った統一的な見方が得られることが射影平面の重要性の一つだと思います。
この見方から得られる面白い応用については今後改めて書いていくことにして、今日はこの辺で終わりにしたいと思います。お読みいただきありがとうございます。
明日はmattyuuさんが楕円曲線について何か書いてくれるそうです!お楽しみに!
$3$は$5$以上のフェルマー素数の原始根
この記事は インテジャーズのadvent calendar 7日目の記事です。
昨日の記事はコロちゃんぬさんによる「インテジャーズと私」というとても面白い記事でした。カスタマーレビューという発想が素晴らしかったです!
こちらの記事では、今年のmathpowerの耐久企画「正$65537$角形の作図」に関連した話題として、フェルマー素数の原始根について書きます。
ご存知のように、素数$p$がフェルマー素数の時、正$p$角形は作図可能です(←インテジャーズ文体を真似したつもりです)。
現在知られているフェルマー素数は$3,5,17,257,65537$の$5$個ですが、これらの$p$について正$p$角形の作図をしようとすると、($p=17$くらいから)$\mathbb{F}_p$の原始根を一つ固定して考えたくなる状況が発生します。
正65537角形の作図方法についてUさんと検討していた時に、こんな感じの会話がありました。
Uさん「$p=17$の原始根って何でしょうね?(計算スラスラ)あー$3$は原始根ですね」
Uさん「$p=257$の原始根って何でしょうね?(PCカタカタ)あ、これも$3$がとれますね」
私「$3$優秀ですねww」
Uさん「じゃあ$p=65537$の原始根はどうなりますかね?」
私「まさか$3$なわけ、、」
Uさん「(PCカタカタ)おっ、これも$3$がとれますね」
私「ええ!?まじですか…!」
実際、$p=17$の時に$3^n \text{ mod }p$は
$$3^1 \equiv 3, 3^2 \equiv 9, 3^3 \equiv 10, 3^4 \equiv 13, 3^5 \equiv 5, 3^6 \equiv 15, 3^7 \equiv 11, 3^8 \equiv 16,$$
$$3^9 \equiv 14, 3^{10} \equiv 8, 3^{11} \equiv 7, 3^{12} \equiv 4, 3^{13} \equiv 12, 3^{14} \equiv 2, 3^{15} \equiv 6, 3^{16} \equiv 1 $$
となっていて、$3$が原始根であることが比較的簡単に確認できます。
その他のフェルマー素数でも計算では確かめられるわけですが、この現象が「偶然なのか、理由があるのか」については、単に計算しただけでははっきりしません。
さて、その後調べ物をしているうちに、この現象には理由が付けられることが分かりました。一般に次の事実が成り立つことが知られています。
定理
$p$が$5$以上のフェルマー素数のとき、$(\mathbb{Z}/p\mathbb{Z})^{\times}$の生成元(原始根)として常に$3$が取れる。
常に、と書きましたが、現在知られている$5$以上のフェルマー素数は$5,17,257,65537$のたった$4$個です。これらの$4$個について$3$が原始根であることは(上記のように)計算すれば確かめられます。
もしフェルマー素数がこれ以降無いことが証明されてしまうと、この定理は威力を発揮しないまま終わってしまう悲しい状態になってしまうので、この事実を知って以降私はフェルマー素数はもっとたくさん存在して欲しいと思うようになりました。もしなんらかの方法で新たなフェルマー素数が発見された時、原始根として計算するまでもなく$3$が取れるのです!
(ただし後述するとおり、この逆に近い事実が成り立っており、これを用いてフェルマー数$F_n=2^{2^n}+1$が素数かどうかの判定を行うこともあるようです(Pépin's test))
ということでこの定理の証明を以下に行います。
(証明)
一般に素数$p$について、$(\mathbb{Z}/p\mathbb{Z})^{\times}$の原始根が常に存在する。それを一つとって$g$とする。任意の$a \in (\mathbb{Z}/p\mathbb{Z})^{\times}$に対して$a = g^{\nu (a)} $なる$\nu (a)$がmod $p-1$で一意に定まり、
$$\left( \frac{a}{p} \right) = (-1)^{\nu (a)} $$
と書ける。ここで $\left( \frac{a}{p} \right)$ は平方剰余記号。
さて、$g$は原始根だから、$g^{\frac{p-1}{2}} \equiv -1 $ mod $p$が成り立ち、
$$\left( \frac{a}{p} \right) = (-1)^{\nu (a)} \equiv (g^{\frac{p-1}{2}})^{\nu (a)}= (g^{\nu (a)})^{\frac{p-1}{2}} = a^{\frac{p-1}{2}} \text{ mod } p $$
が成り立つ(いわゆるEulerの規準)。
さて、$3$が原始根であることを言うには、$3^{\frac{p-1}{2}} \equiv -1 \text{ mod } p$を言えば良いが、上記により
$$\left( \frac{3}{p} \right) = -1 $$
を言えば良いことになる。ここで平方剰余の相互法則が使えて
$$\left( \frac{3}{p} \right) = (-1)^{\frac{3-1}{2}\frac{p-1}{2}} \left( \frac{p}{3} \right) = (-1)^{\frac{p-1}{2}} \left( \frac{p}{3} \right) $$
が成り立つが、今 $p = 2^{2^n}+1 \hspace{3mm} (n \geq 1)$より$\frac{p-1}{2} = 2^{2^n-1}$は偶数だから
$$\left( \frac{3}{p} \right) = \left( \frac{p}{3} \right) $$
となる。また、$p = 2^{2^n}+1 \equiv (-1)^{2^n}+1 =2 \text{ mod } 3$だから結局
$$\left( \frac{3}{p} \right) = \left( \frac{2}{3} \right) =-1 $$
となる。以上より
$$3^{\frac{p-1}{2}} \equiv -1 \text{ mod } p$$が言えた。よって$3$は原始根である。
(証明終了)
さて、以上が証明になりますが、もう少し調べると(といってもwikipediaに書いてる事実だったのですが)、この逆に近いことも言えることが分かりました。すなわち
定理
$n \geq 1$に対し、$F_n$を$F_n=2^{2^n}+1$と定める。$F_n$が素数であることと、$3^{\frac{F_n-1}{2}} \equiv -1 \text{ mod } F_n$が成り立つことは同値。
と興奮気味に書きましたが、この証明は簡単です。必要性は上記の証明の中で示しています。十分性について書きます。
(十分性の証明)
$3^{\frac{F_n-1}{2}} \equiv -1 \text{ mod } F_n$が成り立つならば、$3^{F_n-1} \equiv 1 \text{ mod } F_n$だから$3$の$(\mathbb{Z}/F_n\mathbb{Z})^{\times}$における位数は$F_n-1=2^{2^n}$の約数であり、$2^k$の形。しかし、$k=2^n-1$では$3^{2^k} = 3^{(F_n-1)/2} \equiv -1 \text{ mod } F_n$だから、$3$の位数はちょうど$2^{2^n}$になる。これは$(\mathbb{Z}/F_n\mathbb{Z})^{\times}$の位数が$2^{2^n}$であることを言っているので、$F_n$は素数である。
(証明終了)
なお、wikipediaを見るとこの事実を用いて$F_n$が$n=7, 8, 10, 13, 14, 20, 22, 24$でフェルマー素数でないことの証明に用いられたことが書いてあります(Pépin's test - Wikipedia)。
以上で終わりとします。ここまでお読みいただきありがとうございます。
明日の記事はせきゅーんさんの記事「Szemerédi3」です!お楽しみに!!